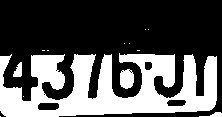Image Processing - Binarization

影像處理是現在多媒體系統或影像監控系統是必備的功能與需求，而在進行諸多處理像是影像辨識等需求時，要對影像進行前置處理其中一樣就是二值化(二值化之前要對影像進行灰階的前置處理)，把影像分成黑或白借此把影像的邊界與形狀取出，剔除相對不重要的資訊。而對於影像處理初出茅廬的我來說這就是一個最好的研究課題。這個領域的知識發展由來已久，而這篇的重點，Otsu演算法，更是這方面的研究論文幾乎必定會比較的方法。（ps.這篇編排先把實驗結果拉到前面實屬特例，這是為了要讓讀著馬上比較兩種演算法的不同，但話說在前頭這兩種方法沒有誰一定比較好）

實驗數據與分析：

原圖來源：Google Image

原圖：

Original

Modified Sauvola:

ModifiedSauvola

Otsu:

Otsu

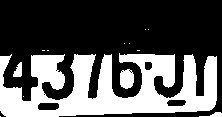
相關研究:

參考文獻：吳乾彌, 許志豪, “影像二值化演算處理器之軟硬整合設計與實現”, 台科大電子工程, 98年六月

paper

這是我在處理影像二值化中最後決定要引用的方法的參考文獻，之前是用鼎鼎大名的Otsu來當作影像閥值的演算法，當初試過一些照片覺得還不錯，但缺點就是閥值的計算是以整張圖片來統計，因此若有區域或局部性的亮度與整體差距過大就會造成該區域整塊的細節消失，算是美中不足的地方。

Otsu

統計整張影像的灰階值，並以此計算值算出以哪個灰階值做劃分可以讓兩群的灰階值的變異數相加為最小，就口語來說就是找出用哪個數值化劃分可以讓兩個群體的群內差距為最小，亦即兩群的差異最大。為了解決 Otsu 的痛處就要使用區域可適應性的閥值選擇方法，讓每個區域選擇自己的閥值，因此就找上了 Sauvola ，這篇，或這篇都有談到這個方法，當然這個方法我有稍稍改了一下，讓他對一個 Window 內的像素值賦予一個閥值，而非每個像素都有一個閥值，這樣可以減少不少計算量，換回不少計算時間。（ps.但是區域可適應性閥值選擇方法因為不像全域性計算一次閥值就好，因此會有比較多的計算時間）

Ostu 的演算法概略如下：

若灰階影像其像速分布為 [1,2,3…x] （註：1~~x 表示灰階影像像素的數值，範圍從 0~~255），可以計算出不同灰階值其分布機率值$P_i$：

$$P_i = n_i / N —(1)$$

其中 $n_i$ 代表灰階值為 i 的個數，$N = n_1+n_2+n_3+…+n_x$ 為所有灰階值個數的總和。而所有$P_i$的總和為1。

$$\sum_{i=1}^xP_i —(2)$$

上述有提到二值化是為了找出閥值讓兩個群體之間的差異最大，群內的差異最小。這裡有兩個群體，G1與G2，G1的灰階值分布為[1,2,3…y]，G2的灰階值分布為[y+1,y+2,y+3,…x]，由此計算出個群集的機率分布W1,W2。

$$W1 = \sum_{i=1}^yP_i —(3)$$

$$W2 = \sum_{i=y+1}^xP_i —(4)$$

接著計算個群集的平均值 M1,M2。

$$M1 = \sum_{i=1}^y i*P_i —(5)$$

$$M2 = \sum_{i=y+1}^x i*P_i —(6)$$

然後就可以利用上述的式子求出個群集的變異數 K1,K2。

$$K1 = \sum_{i=1}^y (i-M1) * (i - M1)*P_i$$

$$K2 = \sum_{i=y+1}^x (i - M1) * (i - M1)*P_i$$

要找到一個閥值可以讓兩個群集的變異數相加最小。

研究方法：

ps.這邊僅列出關鍵的部份。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//#region 計算各灰階值出現的機率。
Int32[] GrayNum = new Int32[256];// 用來記錄灰階值的矩陣，這邊假設已經都匯入完畢
IEnumerator enumerator = GrayNum.GetEnumerator();
List<Double> Property = new List<Double>(256);

while (enumerator.MoveNext())
{
    Property.Add((Int32)enumerator.Current / TotalPixel);
}
//#endregion

//#region 計算累積分佈函數。
Double[] w0 = new Double[256];
w0[0] = Property[0];

for (Int32 num = 1; num < Property.Count; ++num)
{
     w0[num] = (w0[num - 1] + Property[num]);
}
//#endregion
//#region 區域變數的宣告。
// Otsu value
Int32 OptimalOtsu = Int32.MinValue;
// 熵值最佳值(越小越好)。
Double entropyvalue = Double.MaxValue;
Double currententropy = Double.MinValue;
// 存放一、二群的機率
Double category1 = Double.MinValue, category2 = Double.MinValue;
// 第一、二群的加權平均數(期望值)。
Double mean1, mean2;
// 第一、二群的變異數。
Double Variance1, Variance2; 

開始計算閥值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 閥值設在端點作用不大...(所以範圍設在1~254之間)
for (Int32 threshold = 1; threshold <= 254; ++threshold)
{
    #region 以各灰階值為閥值來計算兩群體的變異數總和。
    // 避免分母為零。
    category1 = w0[threshold] < 1e-9 ? 1e-9 : w0[threshold];
    category2 = (1.0 - category1) < 1e-9 ? 1e-9 : (1.0 - category1);

    // 初始化區域變數。
    mean1 = mean2 = 0.0;
    Variance1 = Variance2 = 0.0;

    // 計算兩群的加權平均數(期望值)
    for (Int32 val = 0; val <= threshold; val++)
        mean1 += val * Property[val] / category1;
    for (Int32 val = threshold + 1; val <= 255; val++)
        mean2 += val * Property[val] / category2;

    // 計算兩群的變異數。
    for (Int32 val = 0; val <= threshold; val++)
        Variance1 += Math.Pow((val - mean1), 2) * Property[val];
    Variance1 /= category1;
    for (Int32 val = threshold + 1; val <= 255; val++)
        Variance2 += Math.Pow((val - mean2), 2) * Property[val];
    Variance2 /= category2;

    currententropy = Variance1 * category1 + Variance2 * category2;
    if (currententropy < entropyvalue)
    {
        entropyvalue = currententropy;
        OptimalOtsu = threshold;
     }
}

結論

使用 Otsu 的好處莫過於計算速度快，理解上面有比較容易，是實作二值化入門方法的不二人選！其實在大多數的情況之下利用Otsu就已經可以把很多灰階影像很好的二值化了，只是在一些極端條件下(ex.不均勻的光源)會導致二值化的效果不彰，也因此才會有後續很多不同的二值化方法衍生出來。

相關研究:#

參考文獻：吳乾彌, 許志豪, “影像二值化演算處理器之軟硬整合設計與實現”, 台科大電子工程, 98年六月#

Otsu#

結論#

參考文獻#

相關研究:

參考文獻：吳乾彌, 許志豪, “影像二值化演算處理器之軟硬整合設計與實現”, 台科大電子工程, 98年六月

Otsu

結論

參考文獻